MTH 103 Notes -- Chapter 3 Section 7
MTH 103 Notes - Chapter 3 Section 7
Objectives
- verify inverse functions
- find inverse functions
- determine whether a function is one-to-one
- understand the characteristics of inverse functions
- graph inverse functions
Lesson
Definition:
The function \(g(x)\) is the inverse of \(f(x)\) if
BOTH
- \((f\circ g)(x) = x\) for every \(x\) in the domain of \(g\). AND
- \((g\circ f)(x) = x\) for every \(x\) in the domain of \(f\).
The inverse of the function \(f\) is denoted by \(f^{-1}\). (Read as "f inverse")
Properties of inverses
- domain of \(f\) = range of \(f^{-1}\)
- range of \(f\) = domain of \(f^{-1}\)
- \((f\circ f^{-1})(x) = x \) or \(f(f^{-1}(x)) = x \)
- \((f^{-1}\circ f)(x) = x \) or \(f^{-1}(f(x)) = x \)
- The graphs of \(f\) and \(f^{-1}\) are symmetric over the line \(y = x\).
- If the point \((a, b)\) is on the graph of \(f\), then the point \((b, a)\) is on the graph of \(f^{-1}\).
Example 1:
Using the definition of inverse,
determine whether \(f(x)=3x\) and \(g(x)=\dfrac{3}{x}\) are inverses of each other.
Solution:
Consider \((f\circ g)(x) = f(g(x)) = 3\left(\dfrac{3}{x}\right) = \dfrac{9}{x}\). Since this is not
the same function as \(x\) we know \(f\) and \(g\) cannot be inverses of one another.
Example 2:
Verify \(g=f^{-1}\) if \(f(x) = 3x + 5\) and \(g(x) = \dfrac{x-5}{3}\).
Sketch a graph of both functions. Will the inverse of a linear function always be a linear function? Explain.
Solution:
There are three parts to this question. First lets verify that \(g\) is the inverse of \(f\)
$$\begin{align*}
f(g(x)) &= 3\left(\dfrac{x-5}{3}\right) + 5 \\
&= (x-5)+5 = x \\
g(f(x)) & = \dfrac{(3x+5)-5}{3} \\
&= \dfrac{3x}{3} = x
\end{align*}$$
Now we can sketch both of them via this
desmos web app. Finally we notice that in this case the inverse
of our linear function \(f(x)=3x+5\) is also a linear function. We are asked to answer the question
"Will the inverse of a linear function always be a linear function?" The answer is
yes and this is
because of the property of inverses that says
The graphs of \(f\) and \(f^{-1}\) are symmetric over the line \(y = x\).
So when you reflect a line (like \(f(x)=3x+5\)) you will get another line.
Technique:
for finding the equation for the inverse of a function \(f\):
- Replace \(f(x)\) with \(y\).
- Interchange \(x\) and \(y\).
- Solve for new \(y\). (If \(y\) is not a function of \(x\), then \(f\) does not have an inverse.)
- Replace \(y\) with \(f^{-1}(x)\).
Finally you should check to make sure you didn't make any mistakes.
Does \(f(f^{-1}(x))=f^{-1}(f(x)) = x\)? Or for a quick, "rough" check use the points \((a, b)\) in and \((b, a)\).
Example 3:
Given \(f(x)=\dfrac{4}{x+7}\) find \(f^{-1}\).
Solution:
Let's follow the technique:
$$\begin{align*}
f(x) &= \dfrac{4}{x+7} \tag{Replace \(f(x)\) with \(y\).}\\
y &= \dfrac{4}{x+7} \tag{Interchange \(x\) and \(y\).} \\
x &= \dfrac{4}{y+7} \tag{Solve for new \(y\).} \\
x(y+7) &= 4 \\
(y+7) &= \dfrac{4}{x} \\
y &= \dfrac{4}{x} - 7 \tag{Replace \(y\) with \(f^{-1}(x)\).} \\
f^{-1}(x) &= \dfrac{4}{x} - 7
\end{align*}$$
Let's verify our work by checking \(f(1) = \dfrac{4}{8} = \dfrac{1}{2}\). Also \(f^{-1}(1/2) = \dfrac{4}{1/2}-7=8-7=1\) so
we have shown that \((1,1/2)\) is a point on \(f\) and \((1/2,1)\) is a point on \(f^{-1}\).
Example 4:
Given \(h(x) = 27x^3-1.\) find \(h^{-1}\).
Solution:
Again follow the technique:
$$\begin{align*}
h(x) &= 27x^3-1 \tag{Replace \(h(x)\) with \(y\).}\\
y &= 27x^3-1 \tag{Interchange \(x\) and \(y\).} \\
x &= 27y^3-1 \tag{Solve for new \(y\).} \\
x+1 &= 27y^3 \\
\dfrac{x+1}{27} &= y^3 \\
\sqrt[3]{\dfrac{x+1}{27}} &= y \\
\dfrac{\sqrt[3]{x+1}}{3} &= y \tag{Replace \(y\) with \(h^{-1}(x)\).} \\
\dfrac{\sqrt[3]{x+1}}{3} &= h^{-1}(x)
\end{align*}$$
Example 5:
Find the inverse of \(f(x) = \dfrac{2x+1}{3x-4}\).
Solution:
The technique!
$$\begin{align*}
f(x) &= \dfrac{2x+1}{3x-4} \tag{Replace \(f(x)\) with \(y\).}\\
y &= \dfrac{2x+1}{3x-4} \tag{Interchange \(x\) and \(y\).} \\
x &= \dfrac{2y+1}{3y-4} \tag{Solve for new \(y\).} \\
x(3y-4) &= 2y+1 \\
3xy-4x &= 2y+1 \\
3xy-2y &= 4x+1 \\
(3x-2)y &= 4x+1 \\
y &= \dfrac{4x+1}{3x-2} \tag{Replace \(y\) with \(f^{-1}(x)\).} \\
f^{-1}(x) &= \dfrac{4x+1}{3x-2}
\end{align*}$$
Example 6:
Given \(f(x)=(x-3)^2\), where \(x\leq 3\), find \(f^{-1}\) and the domain of \(f^{-1}\).
Solution:
Two parts this time. First lets find the inverse using the technique:
$$\begin{align*}
f(x) &= (x-3)^2 \tag{Replace \(f(x)\) with \(y\).}\\
y &= (x-3)^2 \tag{Interchange \(x\) and \(y\).} \\
x &= (y-3)^2 \tag{Solve for new \(y\).} \\
\pm\sqrt{x} &= y-3 \\
3\pm\sqrt{x} &= y
\end{align*}$$
Now remember this has to be a function so we must choose either plus or minus. Since \(x\leq 3\) we need to
to choose the negative option. We can verify this with a graph too!
$$\begin{align*}
3 - \sqrt{x} &= y \tag{Replace \(y\) with \(f^{-1}(x)\).} \\
3 - \sqrt{x} &= f^{-1}(x)
\end{align*}$$
Now that we have the inverse we can find its domain by observing that \(\sqrt{x}\) requires \(x\geq 0\)
in order to yeild a real number output. Therefore we can conclude that the domain is \([0,\infty)\). Alternatively
we could use the range of \(f\) (thanks to a property 2 of inverses) to see that the domain of \(f^{-1}\) is
indeed \([0,\infty)\).
Example 7:
Find the inverse of the function \(C(F) = \dfrac{5}{9}(F-32)\).
Solution:
Use the technique:
$$\begin{align*}
C(F) &= \dfrac{5}{9}(F-32) \tag{Replace \(C(F)\) with \(y\).}\\
y &= \dfrac{5}{9}(F-32) \tag{Interchange \(F\) and \(y\).} \\
F &= \dfrac{5}{9}(y-32) \tag{Solve for new \(y\).} \\
\dfrac{9}{5} F &= y-32 \\
\dfrac{9}{5} F +32 &= y \tag{Replace \(y\) with \(C^{-1}(F)\).} \\
\dfrac{9}{5} F +32 &= C^{-1}(F)
\end{align*}$$
Recall:
- The Vertical Line Test (VLT) can be used to see if \(f\) is a function.
- The Horizontal Line Test (HLT) can be used to see if \(f^{-1}\) is a function.
Definition:
A function is called a one-to-one function if it passes both HLT and VLT.
Example 8:
View the graph of each relation and determine whether it represents a one-to-one function.
- The graph of \(x^2+y^2=4\quad\) View desmos graph
- The graph of \(y=x^2-4\quad\) View desmos graph
- The graph of \(y=x^3\quad\) View desmos graph
- The graph of \(y^2-x^2=4\quad\) View desmos graph
Solution:
- No, it does not pass HLT or the VLT
- No, it does not pass HLT
- Yes, it passes both HLT and the VLT
- No, it does not pass HLT or the VLT
Example 9:
Use only the equation given to determine whether it represents a one-to-one function.
- \(f(x)=5x\)
- \(f(x)=2x^2-7\)
- \(h(x)=|x-3|\)
- \(g(x)=3\)
- \(f(x)=(x-4)^2, \; x\geq 4\)
Solution:
- Yes, \(f(x)\) is a line (and is not vertical or horizontal) so it is one-to-one
- No, for instance \(f(1) = 2-7=-5\) and \(f(-1)=2-7=-5\) so there are two \(x\) values that give the same
\(y\) value to \(f\) will not pass the HLT.
- No, for instance \(h(1) =|1-3| =2\) and \(h(5)=|5-3|=2\) so there are two \(x\) values that give the same
\(y\) value to \(h\) will not pass the HLT.
- No, for instance \(f(1) = 3\) and \(f(0)= 3\) so there are two \(x\) values that give the same
\(y\) value to \(f\) will not pass the HLT.
- Yes, it is a function so we know it passes the VLT. It passes the HLT because of the restriction \(x\geq 4\).
Example 10:
Use the graph of \(h\) below to draw the graph of \(h^{-1}\).
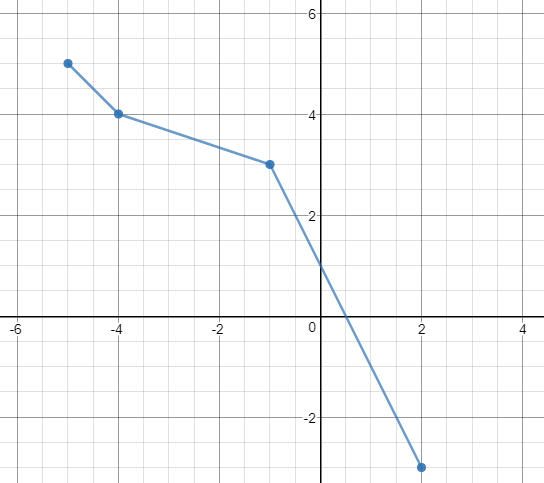
Click the graph for an interactive/accessible version
Solution:
The graph of \(h\) is determined by
connecting points with straight lines. To graph
the inverse we would need to use property 6 of inverses and connect the points
| \(x\) | \(h^{-1}\) |
|---|
| \(5\) | \(-5\) |
| \(4\) | \(-3\) |
| \(3\) | \(-1\) |
| \(-3\) | \(2\) |
Put it all together to get
the graph of the inverse.
Example 11:
Refer to the graph to complete the statements below.
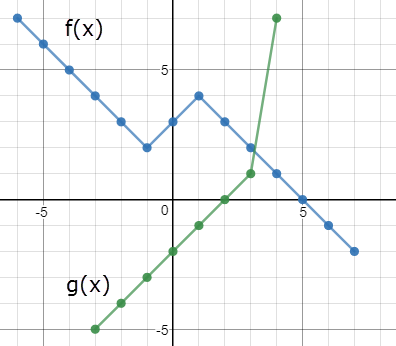
Click the graph for an interactive/accessible version
- Find \((f+g)(-3)\)
- Find \((f\cdot g)(2)\)
- Find \(\left(\dfrac{f}{g}\right)\!(-1)\)
- Find \((f\circ g)(3)\)
- Find \(g^{-1}(-4)\)
- Evaluate \((f\circ f)(2)\)
- Evaluate \(g(f(g(1)))\)
- State the domain of \(f+g\)
- State the domain of \(\dfrac{f}{g}\)
- Which function is a one-to-one function?
- Evaluate \((f(3))^3-4g(-2)\)
- For what value(s) of \(x\) is \(f(x)=3\)?
Solution:
- \((f+g)(-3)=f(-3)+g(-3) = 4-5 = -1\)
- \((f\cdot g)(2) = f(2)\cdot g(2) = 3\cdot 0 =0\)
- \(\left(\dfrac{f}{g}\right)\!(-1) = \dfrac{f(-1)}{g(-1)}=\dfrac{2}{-3}\)
- \((f\circ g)(3) = f(g(3))=f(1)=4\)
- \(g^{-1}(-4) = -2\)
- \((f\circ f)(2) = f(f(2))=f(3)=2\)
- \(g(f(g(1)))=g(f(-1))=g(2)=0\)
- The domain of \(f+g\) is \([-3,4]\)
- The domain of \(\dfrac{f}{g}\) is \([-3,2)\cup(2,4]\)
- \(g\) is a one-to-one function since it passes HLT and VLT.
- \((f(3))^3-4g(-2) = (2)^3 - 4(-4) = 8+16=24\)
- \(f(x)=3\) when \(x=-2, x=0, x=2\)